将正整数表示为若干平方数之和 Perfect Squares

https://leetcode.com/problems/perfect-squares/

Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, …) which sum to n.
Example 1:
Input: n = 12 Output: 3 Explanation: 12 = 4 + 4 + 4.
Example 2:
Input: n = 13 Output: 2 Explanation: 13 = 4 + 9.

动态规划

$$ f(i) = \min\{f(i - s)\} + 1, 其中 s 为平方数且 1 \le s \le i$$

class Solution {
public:
  int numSquares(int n);

private:
  static std::vector<int> &getNums();
  static const int Max = std::numeric_limits<int>::max();
};

std::vector<int> &Solution::getNums() {
  static std::vector<int> Nums{0};
  return Nums;
}

int Solution::numSquares(int n) {
  assert(n > 0);
  auto &Nums = getNums();
  if (Nums.size() > n)
    return Nums[n];
  for (int N, I, Diff, Num; (N = Nums.size()) <= n;) {
    for (I = 1, Num = Max; (Diff = N - I * I) >= 0; ++I)
      Num = std::min(Num, Nums[Diff] + 1);
    Nums.push_back(Num);
  }
  return Nums[n];
}

宽度优先搜索

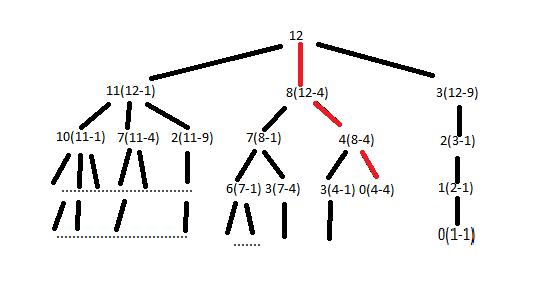
图片来自 Short Python solution using BFS - LeetCode Discuss

int Solution::numSquares(int n) {
  assert(n > 0);
  std::unordered_set<int> Set({n}), Tmp;
  std::vector<int> Squares;
  for (int I = 1, S; (S = I * I) <= n; ++I)
    Squares.push_back(S);
  for (int Level = 1; !Set.empty(); ++Level) {
    for (const auto &N : Set) {
      for (const auto &S : Squares) {
        if (N == S)
          return Level;
        if (N < S)
          break;
        else
          Tmp.insert(N - S);
      }
    }
    Set.clear();
    std::swap(Set, Tmp);
  }
  return -1;
}

筛法

灵感来源于埃拉托斯特尼筛法。Discuss 区翻了一下，好像没人提到过。

1 2 3 4 5 6 7 8 9 10 11 12 13    // numbers
1     1         1                // squares
  2     2     2   2        2     // sums of 2 squares
    3     3     3    3  3        // sums of 3 squares
            4                    // sums of 4 squares

先找出所有平方数，再依次筛选出 2 个、3 个、…、k 个平方数的和。实际上 k 是不会超过 4 的，下一节会提到。

int Solution::numSquares(int n) {
  assert(n > 0);
  std::vector<int> Nums(n + 1);
  std::vector<int> Squares;
  for (int I = 1, Square; (Square = I * I) <= n; ++I) {
    Nums[Square] = 1;
    Squares.push_back(Square);
  }
  if (Nums[n] != 0)
    return 1;
  std::vector<int> Pre = Squares, Cur;
  for (int K = 2, Sum;; ++K) {
    for (const auto &Square : Squares) {
      for (const auto &I : Pre) {
        if ((Sum = Square + I) > n || Nums[Sum] != 0)
          continue;
        Nums[Sum] = K;
        Cur.push_back(Sum);
        if (Sum == n)
          return K;
      }
    }
    std::swap(Pre, Cur);
    Cur.clear();
  }
}

四平方和定理

数学武器可以说是降维打击了。这里用到：

四平方和定理：任何自然数都可以表示为 4 个平方数之和
三平方和定理：对自然数 n ，当且仅当 n 无法表示为 $n = 4^a(8b + 7)$，其中 a、b 为整数，n 可以表示为 3 个平方数之和

由此可以推出：

如果自然数 n 是 4 的倍数，$\frac{n}{4}$ 的结果与其相同
当且仅当自然数 n 可以表示为 $n = 4^a(8b + 7)$ 时（a、b 为整数），n 只能表示为 4 个平方数之和

接下来只需判断 n 是否为 1 或 2 个平方数之和即可，如果不是则只能表示为 3 个平方数之和。

int Solution::numSquares(int n) {
  assert(n > 0);
  while (n % 4 == 0)
    n /= 4;
  if (n % 8 == 7)
    return 4;
  for (int I = 0, S, SE = n / 2, J; (S = I * I) <= SE; ++I) {
    J = static_cast<int>(sqrt(n - S));
    if (S + J * J == n)
      return (I != 0) + (J != 0);
  }
  return 3;
}

时间复杂度 $O(\log(n))$，空间复杂度 $O(1)$。

实现源码

https://github.com/qianbinbin/leetcode

将正整数表示为若干平方数之和 Perfect Squares

动态规划

宽度优先搜索

筛法

四平方和定理

实现源码

参考资料